Detailed problem statement can be found here Gambler's Ruin
General solution to the problem is;
$1- a_1 = a_1 \sum\limits_{i = 1}^{k-1} \left(\frac{1 - p}{p}\right)^i$
For a fair game of $p = \frac{1}{2}$, $a_1 = \frac{1}{k}$
and, for an unfair game of $p \neq \frac{1}{2}$
$a_1 =\frac{\left(\frac{1-p}{p}\right)-1}{\left(\frac{1-p}{p}\right)^k-1}$
Below is the python implementation of the simulation of a fair game of probability $\frac{1}{2}$, with player 1 balance of $98 & player 2 balance of $2
# -*- coding: utf-8 -*-
import numpy as np
number_of_simulations = 1000
# Create an array of wins of length equal to number_of_simulations
wins = [False] * number_of_simulations
# Fair Game
prob = 0.5
p1_balance = 98
p2_balance = 2
for i in range(number_of_simulations):
p1b = p1_balance
p2b = p2_balance
# Play until p1 or p2 is getting ruined
while p1b > 0 and p2b > 0:
p1_win = np.random.uniform(0, 1) < prob
p1b = p1b + 1 if p1_win else p1b - 1
p2b = p2b - 1 if p1_win else p2b + 1
# Set to True, if p1 still not ruined
wins[i] = p1b > 0
prob_p1_wins = sum(wins)/number_of_simulations
print(f'Player 1\'s probability of wining is: {prob_p1_wins}')
Output is;
Player 1's probability of wining is: 0.979
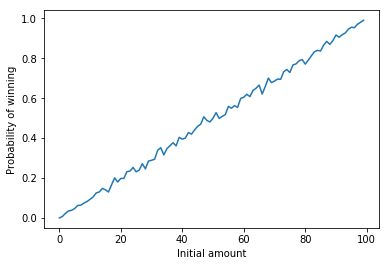
On repeatedly running the above simulation for the player 1 balance ranging from 1 to 99, we will see that probability increases as the initial amount increases;